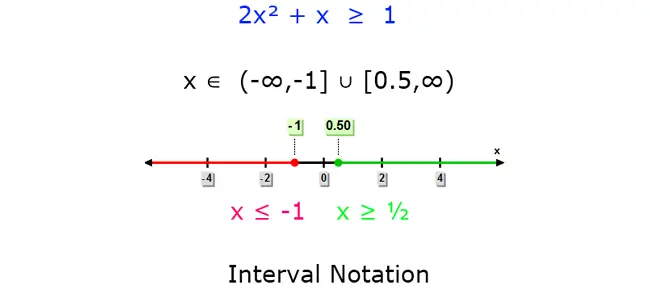
An interval notation is a mathematical method of writing down a set of numbers along an axis. It is also used to describe a specific group of numbers along the X-Axis. In another way, it may be synonymous to a way of writing subsets of the real number line. Looking at the linear equation, the subset is a number contained within a number or the number preceding a certain number. It is derived from the set theory wherein the relationship of each number is called inclusion or containment. The real number line is located at the right side of the X-Axis. It is composed of positive numbers from the origin or center of the linear equation.
Interval notation may be expressed by using the parenthesis “()†which means “not included†or the bracket “[]â€, which means “closed.†Hence, it may be written as [2, 6). When expressed as an inequality it will be shown as 2 ≤ x < 6.
There are many types of interval notation. Open interval means that the endpoints of an ordered pair are not included. Closed interval means that the endpoints are included. Thus, it is expressed as [a, b] or a < x < b. Half-open interval means that the first integer is not included but the second is included. For example, (a, b] is written as a < x < b. Non-ending interval is that the first integer is included but the second is infinity. Some other intervals may require a combination of interval notation to arrive at a certain set of numbers.
Interval notation is an important aspect of mathematics, especially in algebra. Knowing how to locate it allows a person to be familiar with the different points of the linear equation. It is also an important precursor prior to learning geometry and trigonometry.