Introduction:

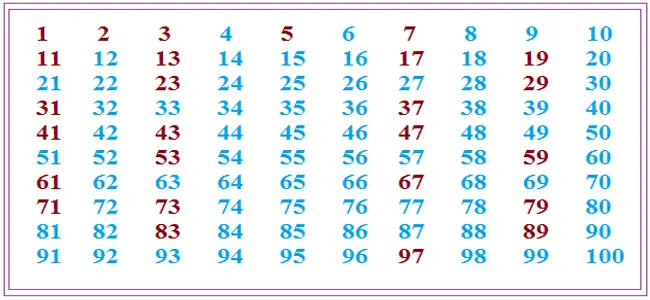
All integers greater than 1 are divided mainly into two groups, prime and Composite numbers. A positive number which has only itself and 1 as factors is a prime number while all other integers belong to the group of Composite Numbers. So, by definition:

A positive integer divisible by another positive number other than itself and 1, is called a Composite Number.

For instance, 9 is a Composite number because it is divisible by 3 apart from 1 and 9 itself. On the other hand, 5 is not a Composite number as its only factors are 1 and itself (5). 5 however, is a Prime number.

Explanation:

Composite numbers are mutually exclusive of Prime numbers i.e. a number cannot be both prime and composite. The exception is the number 1 which is neither prime nor composite. A composite number can always be identified by whether it can be written as a product of two positive integers in at least two different ways where one possible way is always to write C=1x C while the other way is

C=mxn Where m, n ϵ Z

Here both m and n are positive integers other than 1 and as we can see from the above equation, both are divisors of C which makes it a composite number.

All composite numbers can be written as a product of two or more prime numbers.Every one of composite numbers can be built by multiplying prime numbers together which is why they are called composite in the first place. For example, the composite number 15 can be built by multiplying the primes 5 x 3, the composite number 48 can be built by multiplying the primes 2 x 2 x 2 x 2 x 3, and so on. This proves that prime numbers are basically the fundamental building blocks from which all other positive integers are formed. In mathematical language, this principle is known as “The Fundamental Theorem of Arithmetic.”

Being able to differentiate between prime and composite numbers is necessary to begin mathematical factorization. Hope this article helped you in getting started.