Area refers to a quantity that shows the extent of two dimensional shapes or figures on a plane. Surface area is the depiction of two dimensional surfaces of an object that has three dimensions. Area may be said to be the quantity of material that has a specified thickness that is necessary to develop a model of a certain shape or the quantity of paint required to cover a certain surface area with one coat. The surface area of a shape may be determined by comparing the form to designs of established size. The standard measurement of an area is expressed in square meters. Shapes that have an area of 3 square meters have similar areas as 3 such squares.
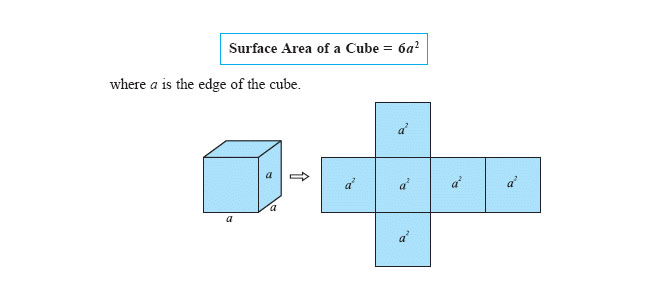
Computing the Surface Area
There are various popular formulas for finding areas of common shapes such as circles, rectangles and triangles. Through these formulas, areas of polygon shapes can be determined when the polygons are divided into triangles. To find the areas of shapes that have curved boundaries, the use of calculus is necessary. To compute the area of solid shapes like cone, spheres and cylinders, one has to compute the surface area which is the area of a shape’s boundary surface. While the surface area of common shapes are computed using the ancient Greek formula, computation of surfaces areas for complicated forms require one to use multivariable calculus.
Importance of Surface Area
In modern day mathematics, area plays a very critical role. Besides the obvious significance in calculus and geometry, area is also related to definition of variables in linear algebra. It is also an elementary aspect of surfaces within differential geometry. Area may be expressed through axioms, which define it as function of various plane figures. Surface area influences planning in construction and manufacturing as it determines cost and quantity functions.